Difference between revisions of "Support:Documents:COMKAT Examples"
(New page: = Example 1: Estimate Input Parameters, Rate Constants Known = Here we assume that the input function has the form Cp = (p1t - p2 - p3) exp(-p4t) + p2 exp(-p5t) + p3 exp(-p6t) where Cp ...) |
|||
| Line 137: | Line 137: | ||
= Simplified reference tissue method = | = Simplified reference tissue method = | ||
| − | |||
This example demonstrates a COMKAT implementation of the simplified reference tissue model (SRTM) described by Lammertsma and Hume [Neuroimage. 4(3 Pt 1), 153-158 (1996)]. By simultaneously analyzing time-activity curves from areas with and without receptors, the SRTM provides a means to estimate the binding potential which is an index of receptor concentration and ligand affinity. | This example demonstrates a COMKAT implementation of the simplified reference tissue model (SRTM) described by Lammertsma and Hume [Neuroimage. 4(3 Pt 1), 153-158 (1996)]. By simultaneously analyzing time-activity curves from areas with and without receptors, the SRTM provides a means to estimate the binding potential which is an index of receptor concentration and ligand affinity. | ||
| − | Background | + | |
| + | ==Background== | ||
Input functions are a fundamental component of pharmacokinetic modeling. They describe the time-course of (radio)pharmaceutical which is accessible to the extravascular space. In PET receptor studies the arterial plasma concentration of a ligand is taken as the input function. As there is desire to obviate blood sampling, the SRTM is a popular method used to analyze ligand-receptor data. | Input functions are a fundamental component of pharmacokinetic modeling. They describe the time-course of (radio)pharmaceutical which is accessible to the extravascular space. In PET receptor studies the arterial plasma concentration of a ligand is taken as the input function. As there is desire to obviate blood sampling, the SRTM is a popular method used to analyze ligand-receptor data. | ||
The typical model equations used for a region containing receptors include state equations for free (F) and bound (B) ligand: | The typical model equations used for a region containing receptors include state equations for free (F) and bound (B) ligand: | ||
| − | dF/dt = k1 Cp | + | <tr> |
| − | dB/dt = k3 F | + | <td width="507">dF/dt = k1 Cp – (k2+k3)F + k4 B </td> |
| − | + | <td width="105">Eq 1 </td> | |
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="507">dB/dt = k3 F – k4 B</td> | ||
| + | <td width="105">Eq 2 </td> | ||
| + | </tr> | ||
where Cp is the arterial plasma input function and tracer conditions are assumed (B << Bmax) so that k3 = kon (Bmax – B) ≈ kon Bmax. | where Cp is the arterial plasma input function and tracer conditions are assumed (B << Bmax) so that k3 = kon (Bmax – B) ≈ kon Bmax. | ||
Model Figure | Model Figure | ||
| − | [[Image:ModelFigure.PNG]] | + | <br>[[Image:ModelFigure.PNG]] |
In a region devoid of receptors, k3 (and therefore B) is zero so Eq 1 may be simplified. Denoting this region as the reference region, or rr, the equation is | In a region devoid of receptors, k3 (and therefore B) is zero so Eq 1 may be simplified. Denoting this region as the reference region, or rr, the equation is | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="52">dF<sub>rr</sub>/dt = k1 Cp – k2<sub>rr</sub> F<sub>rr</sub> </td> | ||
| + | <td width="105">Eq 3 </td> | ||
| + | </tr> | ||
| + | </table> | ||
This may be rearranged to obtain an expression for the plasma input | This may be rearranged to obtain an expression for the plasma input | ||
| − | Cp = Cpn / | + | <table width="622" border="0"> |
| + | <tr> | ||
| + | <td width="507" height="52"> Cp = Cpn / k1<sub>rr</sub></td> | ||
| + | <td width="105">Eq 4 </td> | ||
| + | </tr> | ||
| + | </table> | ||
where | where | ||
| − | Cpn = ( | + | <table width="622" height="66" border="0"> |
| + | <tr> | ||
| + | <td width="507" height="52"> Cpn = (dF<sub>rr</sub>/dt + k2<sub>rr</sub> F<sub>rr</sub>)</td> | ||
| + | <td width="105">Eq 5 </td> | ||
| + | </tr> | ||
| + | </table> | ||
is the normalized plasma input function. | is the normalized plasma input function. | ||
This expression (Eq 4) for Cp may be substituted into the equations for regions that have receptors, aka, target tissue which we denote as tt | This expression (Eq 4) for Cp may be substituted into the equations for regions that have receptors, aka, target tissue which we denote as tt | ||
| − | + | <table width="622" border="0"> | |
| − | + | <tr> | |
| + | <td width="507" height="52">dF<sub>tt</sub>/dt = (k1<sub>tt</sub>/k1<sub>rr</sub>) Cpn – (k2<sub>tt</sub>+k3<sub>tt</sub>)F<sub>tt</sub> + k4<sub>tt</sub> B<sub>tt</sub> </td> | ||
| + | <td width="105">Eq 6 </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td width="507" height="47">dB<sub>tt</sub>/dt = k3<sub>tt</sub> F<sub>tt</sub> – k4<sub>tt</sub> B<sub>tt</sub></td> | ||
| + | <td width="105">Eq 7 </td> | ||
| + | </tr> | ||
| + | </table> | ||
Data from target tissue and from reference regions could be, in theory, simultaneously fit using the model embodied in Eq. 4 to 6. In practice there is often an issue of identifiability. Hence, assumptions are made to reduce the number of parameters to estimate. One assumption is that the equilibrium concentration ratio between plasma and tissue free space is the same in the reference region and target tissue: | Data from target tissue and from reference regions could be, in theory, simultaneously fit using the model embodied in Eq. 4 to 6. In practice there is often an issue of identifiability. Hence, assumptions are made to reduce the number of parameters to estimate. One assumption is that the equilibrium concentration ratio between plasma and tissue free space is the same in the reference region and target tissue: | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="52">k1<sub>tt</sub>/ k2<sub>tt</sub>= k1<sub>rr</sub> /k2<sub>rr</sub></td> | ||
| + | <td width="105">Eq 8 </td> | ||
| + | </tr> | ||
| + | </table> | ||
this implies | this implies | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="52">k1<sub>tt</sub>/k1<sub>rr</sub> = k2<sub>tt</sub>/k2<sub>rr</sub></td> | ||
| + | <td width="105">Eq 9 </td> | ||
| + | </tr> | ||
| + | </table> | ||
and this ratio may be denoted by R1 | and this ratio may be denoted by R1 | ||
| − | R1 = | + | <table width="622" border="0"> |
| + | <tr> | ||
| + | <td width="507" height="52">R1 = k1<sub>tt</sub>/k1<sub>rr</sub> = k2<sub>tt</sub>/k2<sub>rr</sub></td> | ||
| + | <td width="105">Eq 10 </td> | ||
| + | </tr> | ||
| + | </table> | ||
Making the substitution into Eq 6 we obtain | Making the substitution into Eq 6 we obtain | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="52">dF<sub>tt</sub>/dt = R1 Cpn – (k2<sub>tt</sub>+k3<sub>tt</sub>)F<sub>tt</sub> + k4<sub>tt</sub> B<sub>tt</sub> </td> | ||
| + | <td width="105">Eq 11 </td> | ||
| + | </tr> | ||
| + | </table> | ||
This equation could be solved simultaneously with Eq. 7 to obtain time-courses of free and bound radioligand. Analytic solutions derived for more general conditions (Eq 1 and 2) are given in the appendix in the document thad describes validation of the COMKAT implementation of the FDG model. Solutions for Ftt and B tt would then be summed to obtain the total concentration in the target tissue which is the quantity measured in an imaging study | This equation could be solved simultaneously with Eq. 7 to obtain time-courses of free and bound radioligand. Analytic solutions derived for more general conditions (Eq 1 and 2) are given in the appendix in the document thad describes validation of the COMKAT implementation of the FDG model. Solutions for Ftt and B tt would then be summed to obtain the total concentration in the target tissue which is the quantity measured in an imaging study | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="52">C<sub>t</sub><sub></sub> = F<sub>tt</sub>+B<sub>tt</sub> </td> | ||
| + | <td width="105">Eq 12 </td> | ||
| + | </tr> | ||
| + | </table> | ||
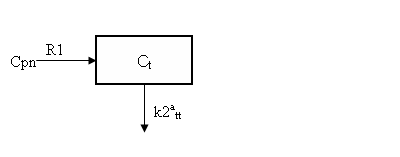
In general, the solution Ctt is a weighted sum of two exponential terms. For ligands in which the association and dissociation of ligand from the receptor is much faster than the transport of ligand between the vascular and extravascular space, two exponentials are not evident from the data. That is, a single exponential model adequaltey describes the data because the two compartments exchange so quickly that they look like a single compartment. (Mathematically one of the eigenvalues or exponential coefficients is very large in magnitude.) The differential equation for such a single-exponential model is | In general, the solution Ctt is a weighted sum of two exponential terms. For ligands in which the association and dissociation of ligand from the receptor is much faster than the transport of ligand between the vascular and extravascular space, two exponentials are not evident from the data. That is, a single exponential model adequaltey describes the data because the two compartments exchange so quickly that they look like a single compartment. (Mathematically one of the eigenvalues or exponential coefficients is very large in magnitude.) The differential equation for such a single-exponential model is | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="45">dC<sub>tt</sub> /dt = k1<sub>tt </sub>Cp –k2<sup>a</sup><sub>tt</sub> C <sub>tt</sub> </td> | ||
| + | <td width="105">Eq 13 </td> | ||
| + | </tr> | ||
| + | </table> | ||
where k2att is the the apparent k2tt and is related to the the other parameters as | where k2att is the the apparent k2tt and is related to the the other parameters as | ||
| − | + | <table width="622" border="0"> | |
| + | <tr> | ||
| + | <td width="507" height="45">k2<sup>a</sup><sub>tt</sub> = k2<sub>tt </sub>/(1+BP)<sub></sub> </td> | ||
| + | <td width="105">Eq 14 </td> | ||
| + | </tr> | ||
| + | </table> | ||
where BP = k3tt/k4tt is the binding potential. Expressing the input in terms of Cpn, this is equivalent to the one-tissue compartment model depicted below | where BP = k3tt/k4tt is the binding potential. Expressing the input in terms of Cpn, this is equivalent to the one-tissue compartment model depicted below | ||
| Line 194: | Line 257: | ||
[[Image:SimplifiedModelFigure.png]] | [[Image:SimplifiedModelFigure.png]] | ||
| − | COMKAT Implementation | + | == COMKAT Implementation == |
comkat\examples\dasbSRTM.m | comkat\examples\dasbSRTM.m | ||
Revision as of 00:15, 7 November 2007
Example 1: Estimate Input Parameters, Rate Constants Known
Here we assume that the input function has the form
Cp = (p1t - p2 - p3) exp(-p4t) + p2 exp(-p5t) + p3 exp(-p6t)
where Cp is the plasma concentration of 18FDG, pi are the input function parameters to be estimated, and t is time. (This form comes from Feng, Huang, Wang. "Models for Computer simulation Studies of Input Functions for Tracer Kinetic Modeling with Positron Emission Tomography", International Journal of Biomedical Computing, 32(2):95-110, March 1993.)
Step 1 To set this up in MATLAB for simulation, create the following function and put it in a file called refCp.m:
function [fval, jac] = refCp(p, t)
if (nargout > 0),
t = t(:); % make it a column vector
fval = (p(1)*t - p(2) - p(3)) .* exp(-p(4)*t) + p(2) * exp(-p(5)*t) + p(3) * exp(-p(6)*t);
if (nargout > 1),
jac = [t .* exp(-p(4)*t) ...
-exp(-p(4)*t) + exp(-p(5)*t) ...
-exp(-p(4)*t) + exp(-p(6)*t) ...
-t .* (p(1)*t - p(2) - p(3)) .* exp(-p(4)*t) ...
-t * p(2) .* exp(-p(5)*t) ...
-t * p(3) .* exp(-p(6)*t)];
end
end
return
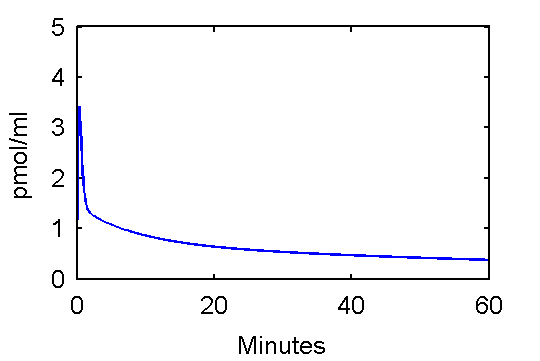
This function can be used to plot an example input curve using these commands
t=0:.1:60;
pin = [28 0.75 0.70 4.134 0.1191 0.01043];
plot(t,refCp(pin,t))
set(gca,'FontSize',6);
axis([0 60 0 5]);
xlabel('Minutes');
ylabel('pmol/ml');
Note that he above function, refCp.m not only calculates values Cp, it also optionally calculates values for the derivative of Cp with respect to parameter vector p. These will be needed later since to fit the input function, it is important to quantify how changes in values of p will effects Cp values which, in turn, effect model-predicted tissue concentration reflected in voxels or regions of interest.
Step 2 Create an FDG model
cm = compartmentModel;
% k1 k2 k3 k4
ktrue=[0.1020 0.1300 0.0620 0.0068];
% define the parameters
cm = addParameter(cm, 'k1', ktrue(1)); % 1/min
cm = addParameter(cm, 'k2', ktrue(2)); % 1/min
cm = addParameter(cm, 'k3', ktrue(3)); % ml/(pmol*min)
cm = addParameter(cm, 'k4', ktrue(4)); % 1/min
cm = addParameter(cm, 'sa', 75); % specific activity of injection, kBq/pmol
cm = addParameter(cm, 'dk', log(2)/109.8); % radioactive decay
cm = addParameter(cm, 'PV', 1); % (none)
% define input function parameter vector
cm = addParameter(cm, 'pin', [28; 0.75; 0.70; 4.134; 0.1191; 0.01043]);
% define compartments
cm = addCompartment(cm, 'Ce', );
cm = addCompartment(cm, 'Cm', );
cm = addCompartment(cm, 'Junk', );
% define plasma input function
% specifying function as refCp with parameters pin
cm = addInput(cm, 'Cp', 'sa', 'dk', 'refCp', 'pin'); % plamsa pmol/ml
% connect inputs and compartments
cm = addLink(cm, 'L', 'Cp', 'Ce', 'k1');
cm = addLink(cm, 'K', 'Ce', 'Junk', 'k2');
cm = addLink(cm, 'K', 'Ce', 'Cm', 'k3');
cm = addLink(cm, 'K', 'Cm', 'Ce', 'k4');
% specify scan begin and end times
ttt=[ ones(6,1)*5/60; ... % 6 frames x 5 sec
ones(2,1)*15/60; ... % 2 frames x 15 sec
ones(6,1)*0.5;... % 6 frames x 0.5 min
ones(3,1)*2;... % 3 frames x 2 min
ones(2,1)*5;... % 2 frames x 5 min
ones(10,1)*10]; % 10 frames x 10 min
scant = [[0;cumsum(ttt(1:(length(ttt)-1)))] cumsum(ttt)];
cm = set(cm, 'ScanTime', scant);
% define an output which is sum of Ce and Cm adjusted to account
% for partial volume (PV). Ignore vascular activity.
Wlist = {...
'Ce', 'PV';
'Cm', 'PV'};
Xlist = {};
cm = addOutput(cm, 'PET', Wlist, Xlist);
% solve model and generate example output
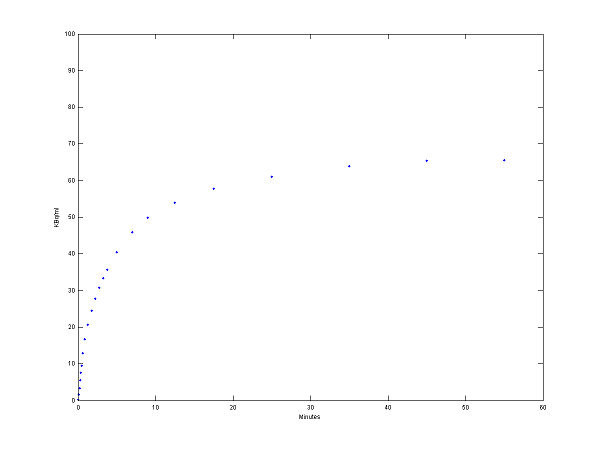
[PET, PETindex]=solve(cm);
plot(0.5*(PET(:,1)+PET(:,2)),PET(:,3), '.');
set(gca,'FontSize',6);
axis([0 60 0 100])
xlabel('Minutes');
ylabel('KBq/ml');
Step 3 Use model output as perfect "data"
data = PET(:,3);
Step 4 Fit the "data"
% tell model abbout data to be fit cm = set(cm, 'ExperimentalData', data); % specify parameters to be adjusted in fitting cm = addSensitivity(cm, 'pin'); % set parameter values initial guess, lower and upper bounds pinit = [ 10; 0.4; 0.4; 3; 0.05; 0.01]; plb = [ 10; 0.1; 0.1; 1; 0.05; 0.001]; pub = [100; 2. ; 2. ; 10; 1. ; 0.05]; % actually do the fitting pfit = fit(cm, pinit, plb, pub);
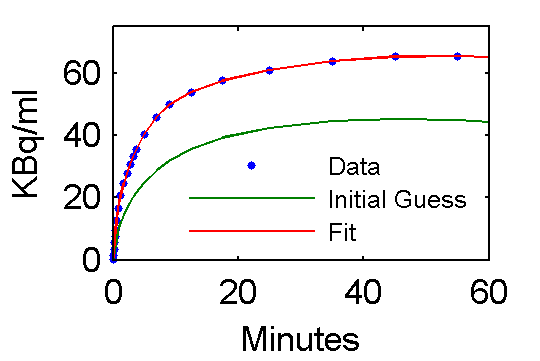
Values of parameter pfit estimates are [28.0167; 0.7652; 0.7059; 4.1586; 0.1257; 0.0105] and are reasonably close to the true values (pxEval(cm, 'pin')) [28; 0.75; 0.70; 4.134; 0.1191; 0.01043]
Step 5 Examine model outputs for "data", initial guess, and fit
PETfit = solve(set(cm, 'ParameterValue', 'pin', pfit));
PETinit = solve(set(cm, 'ParameterValue', 'pin', pinit));
t = 0.5*(PET(:,1)+PET(:,2));
plot(t,data,'.', t, PETinit(:,3), t, PETfit(:,3));
set(gca,'FontSize',8);
axis([0 60 0 75])
xlabel('Minutes');
ylabel('KBq/ml');
ah=legend('Data', 'Initial Guess', 'Fit','Location','SouthEast');
set(ah,'FontSize',6,'Box','off');
Simplified reference tissue method
This example demonstrates a COMKAT implementation of the simplified reference tissue model (SRTM) described by Lammertsma and Hume [Neuroimage. 4(3 Pt 1), 153-158 (1996)]. By simultaneously analyzing time-activity curves from areas with and without receptors, the SRTM provides a means to estimate the binding potential which is an index of receptor concentration and ligand affinity.
Background
Input functions are a fundamental component of pharmacokinetic modeling. They describe the time-course of (radio)pharmaceutical which is accessible to the extravascular space. In PET receptor studies the arterial plasma concentration of a ligand is taken as the input function. As there is desire to obviate blood sampling, the SRTM is a popular method used to analyze ligand-receptor data.
The typical model equations used for a region containing receptors include state equations for free (F) and bound (B) ligand:
dF/dt = k1 Cp – (k2+k3)F + k4 B
Eq 1
dB/dt = k3 F – k4 B
Eq 2
where Cp is the arterial plasma input function and tracer conditions are assumed (B << Bmax) so that k3 = kon (Bmax – B) ≈ kon Bmax.
Model Figure
In a region devoid of receptors, k3 (and therefore B) is zero so Eq 1 may be simplified. Denoting this region as the reference region, or rr, the equation is
| dFrr/dt = k1 Cp – k2rr Frr | Eq 3 |
This may be rearranged to obtain an expression for the plasma input
| Cp = Cpn / k1rr | Eq 4 |
where
| Cpn = (dFrr/dt + k2rr Frr) | Eq 5 |
is the normalized plasma input function.
This expression (Eq 4) for Cp may be substituted into the equations for regions that have receptors, aka, target tissue which we denote as tt
| dFtt/dt = (k1tt/k1rr) Cpn – (k2tt+k3tt)Ftt + k4tt Btt | Eq 6 |
| dBtt/dt = k3tt Ftt – k4tt Btt | Eq 7 |
Data from target tissue and from reference regions could be, in theory, simultaneously fit using the model embodied in Eq. 4 to 6. In practice there is often an issue of identifiability. Hence, assumptions are made to reduce the number of parameters to estimate. One assumption is that the equilibrium concentration ratio between plasma and tissue free space is the same in the reference region and target tissue:
| k1tt/ k2tt= k1rr /k2rr | Eq 8 |
this implies
| k1tt/k1rr = k2tt/k2rr | Eq 9 |
and this ratio may be denoted by R1
| R1 = k1tt/k1rr = k2tt/k2rr | Eq 10 |
Making the substitution into Eq 6 we obtain
| dFtt/dt = R1 Cpn – (k2tt+k3tt)Ftt + k4tt Btt | Eq 11 |
This equation could be solved simultaneously with Eq. 7 to obtain time-courses of free and bound radioligand. Analytic solutions derived for more general conditions (Eq 1 and 2) are given in the appendix in the document thad describes validation of the COMKAT implementation of the FDG model. Solutions for Ftt and B tt would then be summed to obtain the total concentration in the target tissue which is the quantity measured in an imaging study
| Ct = Ftt+Btt | Eq 12 |
In general, the solution Ctt is a weighted sum of two exponential terms. For ligands in which the association and dissociation of ligand from the receptor is much faster than the transport of ligand between the vascular and extravascular space, two exponentials are not evident from the data. That is, a single exponential model adequaltey describes the data because the two compartments exchange so quickly that they look like a single compartment. (Mathematically one of the eigenvalues or exponential coefficients is very large in magnitude.) The differential equation for such a single-exponential model is
| dCtt /dt = k1tt Cp –k2att C tt | Eq 13 |
where k2att is the the apparent k2tt and is related to the the other parameters as
| k2att = k2tt /(1+BP) | Eq 14 |
where BP = k3tt/k4tt is the binding potential. Expressing the input in terms of Cpn, this is equivalent to the one-tissue compartment model depicted below
COMKAT Implementation
comkat\examples\dasbSRTM.m
Step 1 To set this up in MATLAB, create an input function that implements Eq. 5 [Cpn = (dFrr/dt + k2rr Frr)]. In this k2rr is a parameter to estimate amd Frris taken as experimentally measured reference region concentration. To obtain Frr at arbitrary times requires interpolation. For this a smoothing spline is used. Its piecewise-polynomial coefficients are easily obtained
ppCref = csaps(tref, Cref, 0.01);
where tref and Cref are the sample times and concentrations from the reference region. With Frr expressed in this form, the polynomials may be analytically differentiated once to obtain the piecewise polynomial coefficients of dFrr/dt
ppdCrefdt = fnder(ppCref, 1);
The input Cpn may be evaluated as Cpn(t) = k2rr x ppval(ppCref. t) + ppval(ppdCrefdt.t) with the complete function given in comkat\examples\refInput.m
function [Cpn, dCpndk2ref] = refInput(k2ref, t, pxtra)
ppCref = pxtra{1};
ppdCrefdt = pxtra{2};
if (nargout > 0),
Cpn = k2ref * ppval(ppCref, t) + ppval(ppdCrefdt,t);
idx = find(Cpn < 0);
Cpn(idx) = 0;
if (nargout > 1),
dCpndk2ref = ppval(ppCref, t);
dCpndk2ref(idx) = 0;
end
end
return
For the sake of estimating the value of k2rr, this function must provide the derivative of Cpn with respect to k2rr when two output arguments are requested.
This input function is included in the compartment model by using these commands
sa = 1; % specific activity
dk = 0; % decay constant (=0 since data are decay corrected)
xparm = { ppCref, ppdCrefdt };
cm = addInput(cm, 'Cpn', sa, dk, 'refInput', 'k2ref', xparm);
Step 2 Create a model. To simultaneously fit three regions – midrbain, amygdala, and thalamus – create a model that has the compartments and links depicted as shown. Three Region Model
The commands are
% specify compartments
cm = addCompartment(cm, 'Cmid');
cm = addCompartment(cm, 'Camy');
cm = addCompartment(cm, 'Ctha');
cm = addCompartment(cm, 'Sink'); % comkat requires closed system
% specify links
cm = addLink(cm, 'L', 'Cpn', 'Cmid', 'R1mid'); % connect input to
cm = addLink(cm, 'K', 'Cmid', 'Sink', 'k2ppmid');
cm = addLink(cm, 'L', 'Cpn', 'Camy', 'R1amy');
cm = addLink(cm, 'K', 'Camy', 'Sink', 'k2ppamy');
cm = addLink(cm, 'L', 'Cpn', 'Ctha', 'R1tha');
cm = addLink(cm, 'K', 'Ctha', 'Sink', 'k2pptha');
% specify outputs (neglect vascular contrib)
% for simultaneously fitting target tissues
cm = addOutput(cm, 'Mid', {'Cmid', 'PV'}, { } );
cm = addOutput(cm, 'Amy', {'Camy', 'PV'}, { } );
cm = addOutput(cm, 'Tha', {'Ctha', 'PV'}, { } );
% specify parameters and values
cm = addParameter(cm, 'PV', 1);
cm = addParameter(cm, 'k2ref', 0.05);
cm = addParameter(cm, 'R1mid', 0.8);
cm = addParameter(cm, 'R1amy', 1.0);
cm = addParameter(cm, 'R1tha', 1.2);
cm = addParameter(cm, 'BPmid', 0.5);
cm = addParameter(cm, 'BPamy', 1.0);
cm = addParameter(cm, 'BPtha', 1.5);
cm = addParameter(cm, 'k2ppmid', 'k2ref*R1mid/(1+BPmid)');
cm = addParameter(cm, 'k2ppamy', 'k2ref*R1amy/(1+BPamy)');
cm = addParameter(cm, 'k2pptha', 'k2ref*R1tha/(1+BPtha)');
The rest of the details are quite straightforward and are all contained in the example file comkat\examples\dasbSRTM.m. The only thing slightly unusual is that multiple time-activity curves must be specified so they can be simultaneously fit. To do this, just use
cm = set(cm, 'ExperimentalData', PETdata(:, [1 2 3]));
where columns [1 2 3] contain 'Mid', 'Amy', and 'Tha' data [the same order as the adddOutput() commands] and the rows of PETdata correspond to different frames.